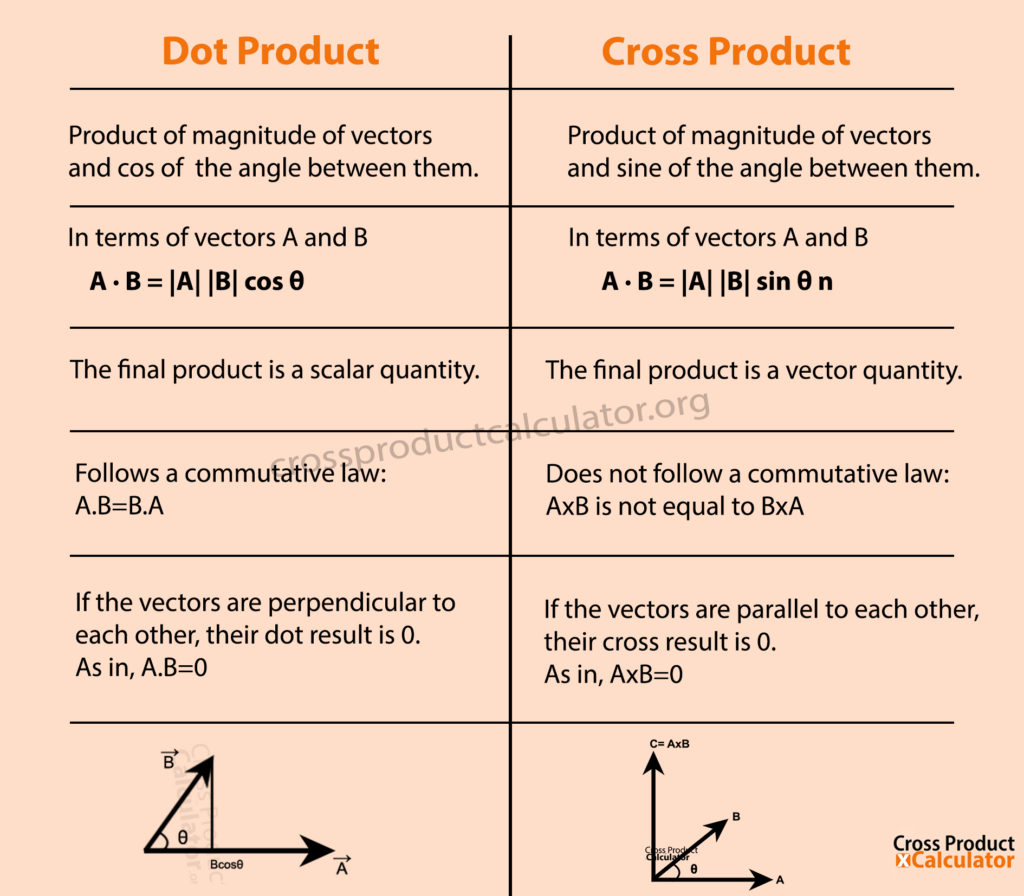
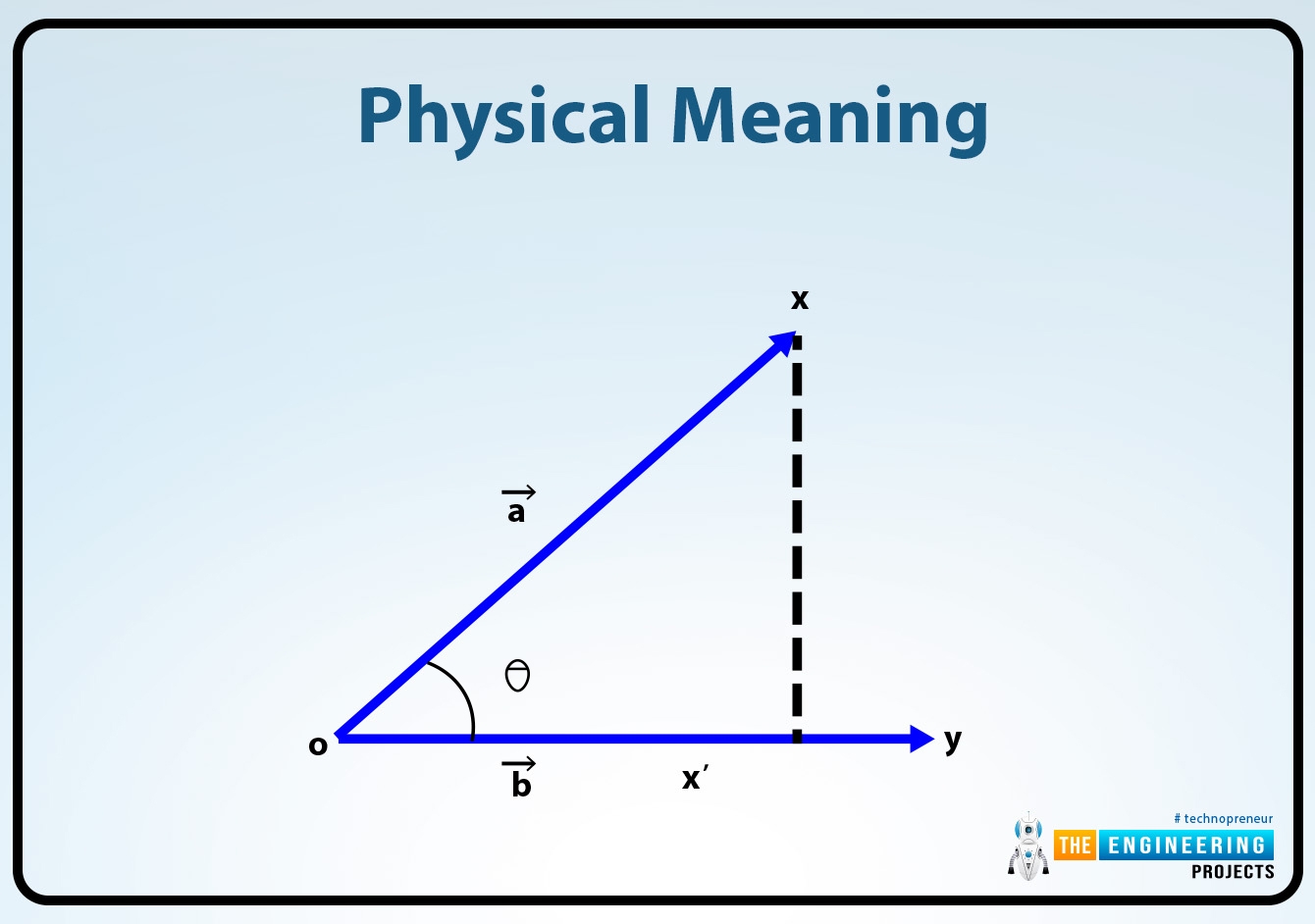
Dot scalar product, also known as the dot product or inner product, is a fundamental operation in linear algebra that takes two vectors and returns a scalar quantity. It is used to measure the similarity or perpendicularity of vectors and is essential in various fields such as physics, engineering, and computer science.
When two vectors are multiplied using the dot product, the result is a single number that represents the projection of one vector onto the other. This can be thought of as the magnitudes of the two vectors multiplied by the cosine of the angle between them. The dot product is denoted by a · b or a⋅b, where a and b are the two vectors.
Calculating the Dot Scalar Product
To calculate the dot product of two vectors a = [a1, a2, a3] and b = [b1, b2, b3], the formula is:
a · b = a1 * b1 + a2 * b2 + a3 * b3
For example, if a = [2, 3, 1] and b = [4, 2, 5], the dot product would be:
2 * 4 + 3 * 2 + 1 * 5 = 8 + 6 + 5 = 19
The result of the dot product in this case is 19, which is a scalar quantity indicating the similarity or projection of the two vectors onto each other.
The dot product can also be used to calculate the angle between two vectors. By rearranging the formula and solving for the angle θ, we get:
cos(θ) = (a · b) / (|a| * |b|)
Where |a| and |b| are the magnitudes of vectors a and b, respectively. This formula can be used to determine if two vectors are parallel (cos(θ) = 1), perpendicular (cos(θ) = 0), or at some other angle.
In conclusion, the dot scalar product is a powerful mathematical operation that is widely used in various fields to measure the similarity, perpendicularity, and angle between vectors. Its simplicity and versatility make it an essential tool for solving complex problems and analyzing relationships between vectors.